La aparición del análisis infinitesimal fue la culminación de un largo proceso, cuya esencia matemática interna consistió en la acumulación y asimilación teórica de los elementos del cálculo diferencial.
Para el desarrollo de este proceso se contaba con el álgebra; las técnicas de cálculo; introducción a las matemáticas variables; el método de coordenadas; ideas infinitesimales clásicas, especialmente de Arquímedes; problemas de cuadraturas y la búsqueda de tangentes. Las causas que motivaron este proceso fueron las exigencias de la mecánica newtoniana y la astronomía.
La última etapa del desarrollo del análisis infinitesimal fue el establecimiento de la relación e inversibilidad mutua entre las investigaciones diferenciales, y a partir de aquí la formación del cálculo diferencial. El cálculo diferencial surgió casi simultáneamente en dos formas diferentes: en la forma de teoría de fluxiones de Newton y bajo la forma del cálculo de diferenciales de G. W. Leibniz.
Relación.
Regla de correspondencia entre los elementos de dos conjuntos.
Esta relación se representa con el siguiente conjunto de pares ordenados.
Función
El concepto de función es uno de los más importantes en el mundo de las matemáticas. Las funciones no sólo representan fórmulas, o lugares geométricos, también se utilizan como modelos matemáticos que resuelven problemas de la vida real.
A continuación se dan algunas definiciones de función:
- Es una regla de correspondencia que asocia a los elementos de dos conjuntos. La cual a cada elemento del primer conjunto (dominio) le asocia un solo elemento del segundo conjunto (contradominio).
- Sean A y B dos conjuntos y 𝑓 una regla que a cada 𝓍 ∈ A asigna un único elemento 𝑓(𝓍) del conjunto B, se dice que 𝑓 es una función que va del conjunto A al B, y se representa de la siguiente forma: 𝑓: A → B, donde al conjunto A se le llama dominio y al B contradominio, que también se representa por medio de un diagrama de flechas:
Como diferenciar una relación de una función.
Ejemplo 1 - Determina si los siguientes diagramas representan una función o una relación:
Solución:
El primer y el tercer diagramas corresponden a una función ya que a cada elemento del conjunto A se le asigna un solo elemento del conjunto B.
En el segundo diagrama al menos a un elemento del conjunto A se le asignan dos elementos del conjunto B, mientras que en el cuarto diagrama el elemento 8 se asocia con tres elementos del conjunto B, por tanto, se concluye que estos conjuntos representan una relación.
Ejemplo 2 - Determina si los siguientes conjuntos de pares ordenados corresponden a una función o a una relación:
Solución:
Los conjuntos A y C son funciones ya que el primer elemento de cada par ordenado no se repite. En el conjunto B el 3 y el 5 aparecen dos veces como primer elemento del par ordenado mientras que en el conjunto M al 2 se le están asignando el 4 y el 6 como segundo elemento, por tanto, B y M son relaciones.
Las funciones y relaciones pueden tener una representación gráfica en el plano cartesiano. Para distinguir si se trata de una función o una relación basta con trazar una recta paralela al eje “Y” sobre la gráfica; si ésta intersecta en dos o más puntos es una relación, si sólo intersecta un punto será una función.
Ejemplo 3 - Determina si las siguientes gráficas representan una relación o una función.
Solución:
Se traza una recta vertical en ambas gráficas y se observa que en la primera intersecta en dos puntos a la gráfica, por tanto, representa una relación y en la segunda, la recta vertical intersecta en un punto a la gráfica, por consiguiente representa una función.
Valor de una función
El valor real 𝑓(𝓍) de una función es aquel que toma y cuando se asigna a 𝓍 un determinado valor real.Ejemplo 1
Ejemplo 2
Ejemplo 3.
Dominio, contradominio y rango de una función.
Dada una función 𝑓: A → B, se dice que el conjunto A es el dominio (D𝑓 ) y B el contradominio (C𝑓 ) o codominio de 𝑓. En términos del plano cartesiano, el dominio corresponde al conjunto formado por los valores posibles para X mientras que el contradominio corresponde a los valores posibles para Y.
Rango (R𝑓)
Valores del contradominio para los cuales y = 𝑓(𝓍), siendo 𝑓(𝓍) la imagen de 𝓍.
Dominio
Grafica, dominio y rango de una función
Fin del tema





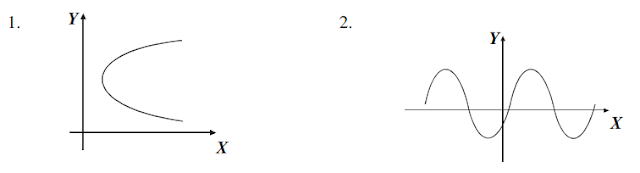




No hay comentarios:
Publicar un comentario